经典算法：蚂蚁走迷宫(一)

本段程序的基本思想是利用蚁群算法中的蚁周模型，来对全局的迷宫图进行信息素的跟新和为每一仅仅蚂蚁选择下一个方格。

故事起源

  有一只蚂蚁出去寻找食物，无意中进入了一个迷宫。蚂蚁只能向上、下、左、右4个方向走，迷宫中有墙和水的地方都无法通行。这时蚂蚁犯难了，怎样才能找出到食物的最短路径呢？

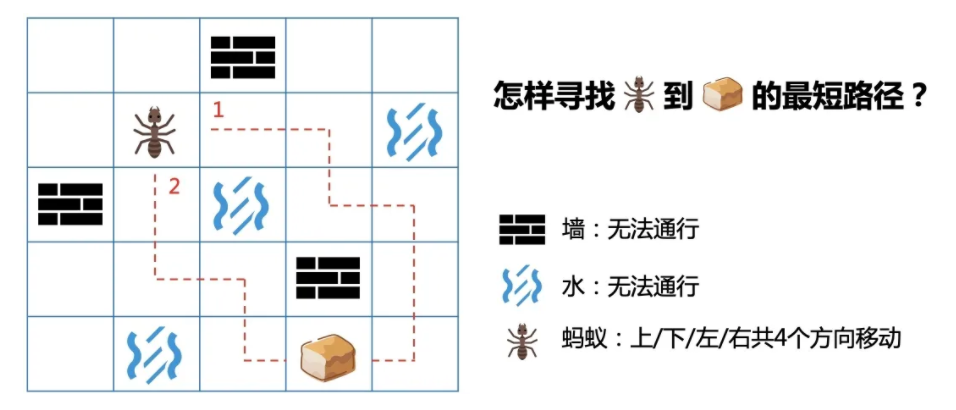
思考

  蚂蚁在起点时，有4个选择，可以向上、下、左、右某一个方向走1步。

如果蚂蚁走过了一段距离，此时也依然只有4个选择。当然要排除之前走过的地方（不走回头路，走了也只会更长）和无法通过的墙和水。

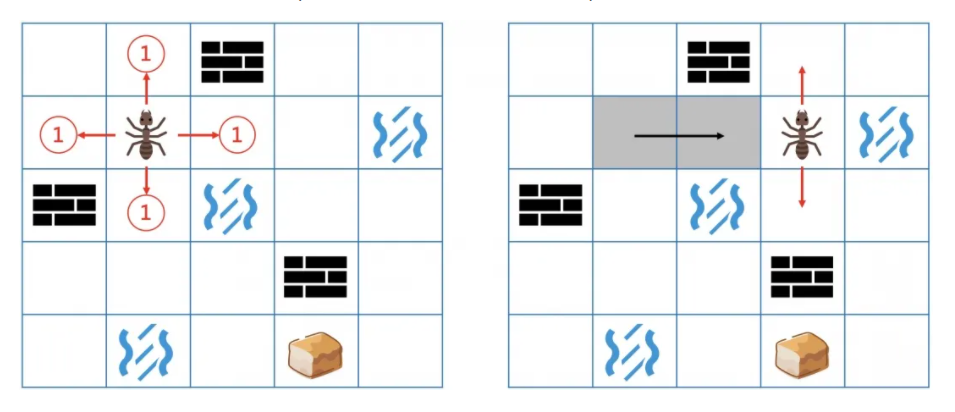
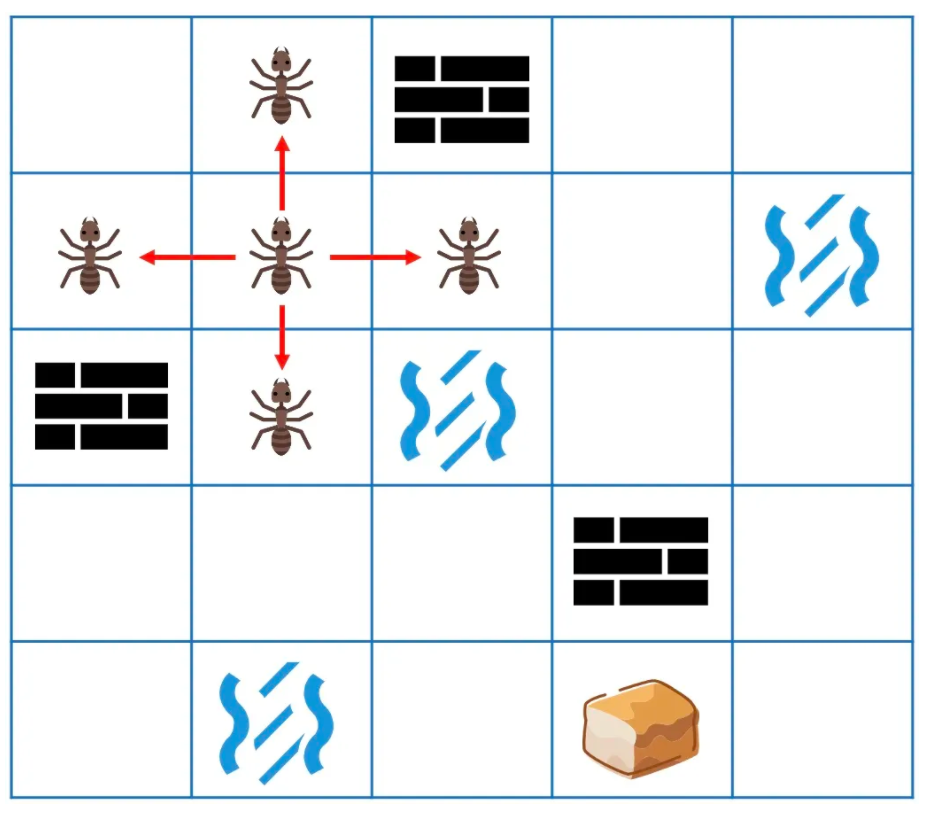
  蚂蚁想，还好我会影分身。如果每一步都分身成4个蚂蚁，向4个方向各走1步，这样最先找到食物的肯定就是最短的路径了（因为每一步都把能走的地方都走完了，肯定找不出更短的路径了）。

  而且还能看出，第1步会到达所有到起点距离为1的地方，第2步也会到达所有距离为2的地方。

如此类推，第n步会覆盖所有到起点最短距离为n的地方。

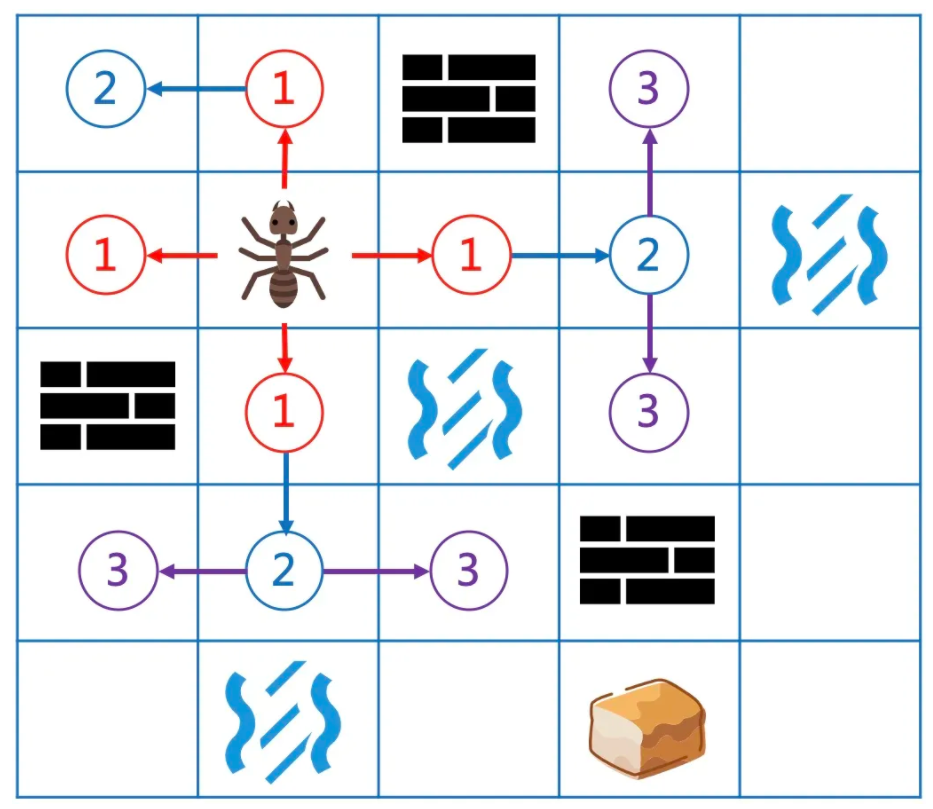
问题建模

迷宫地图放在二维数组中，能通行的地方为0，墙和水的地方为负数。

每一步向4个方向走，可以通过当前坐标加上一个方向向量。

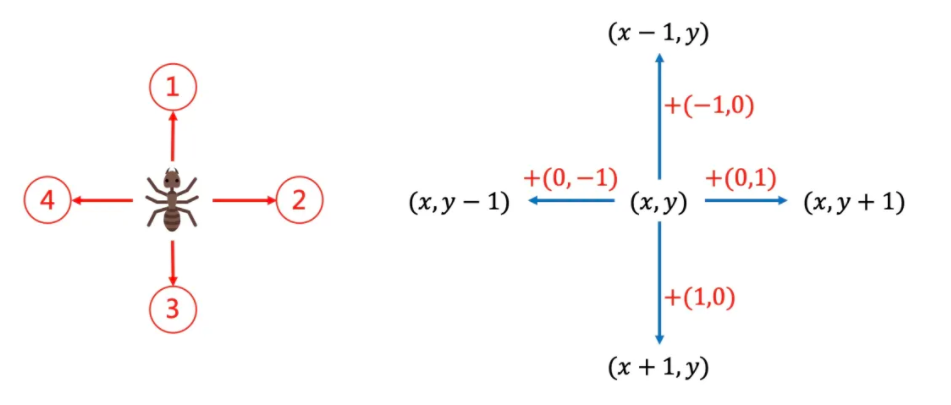
这个其实就是宽度优先搜索(BFS)的思想。

宽度优先搜索(BFS)

又称广度优先搜索，优先向四周扩展子节点，是最简便的图的搜索算法之一，一般通过队列来实现。

队列

是一种特殊的线性表，它只允许在表的前端进行删除操作，而在表的后端进行插入操作，即先进先出。

队列一般通过数组实现，对该数组增加一些操作上的限制。

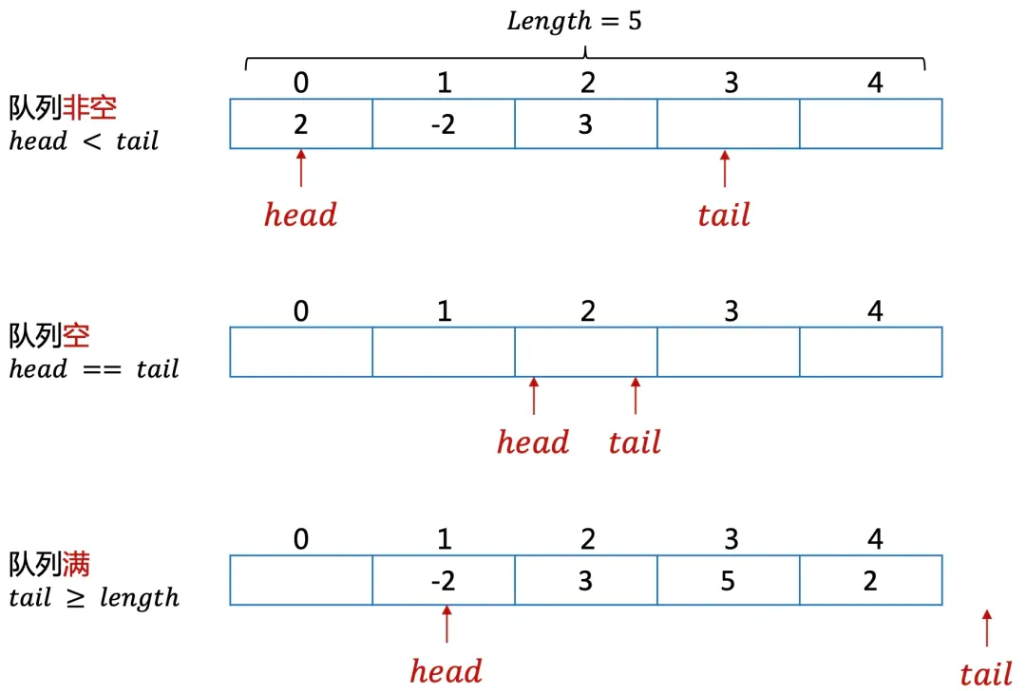
但上面的实现有一些缺陷，当队列满时，也就是tail指针移动到队尾，这时就无法再插入数据，但前面的元素已经出队了，可能还有空缺的位置。

为了能高效利用空间，对该队列增加一点改进，也就是循环队列的产生。

循环队列

把队列想象成一个首尾相接的环形。

数组实现，需要多预留一个空间。如果head=tail时，无法判断是队空还是队满，所以占用一个空间，通过tail+1与head的关系来判断是否队满。

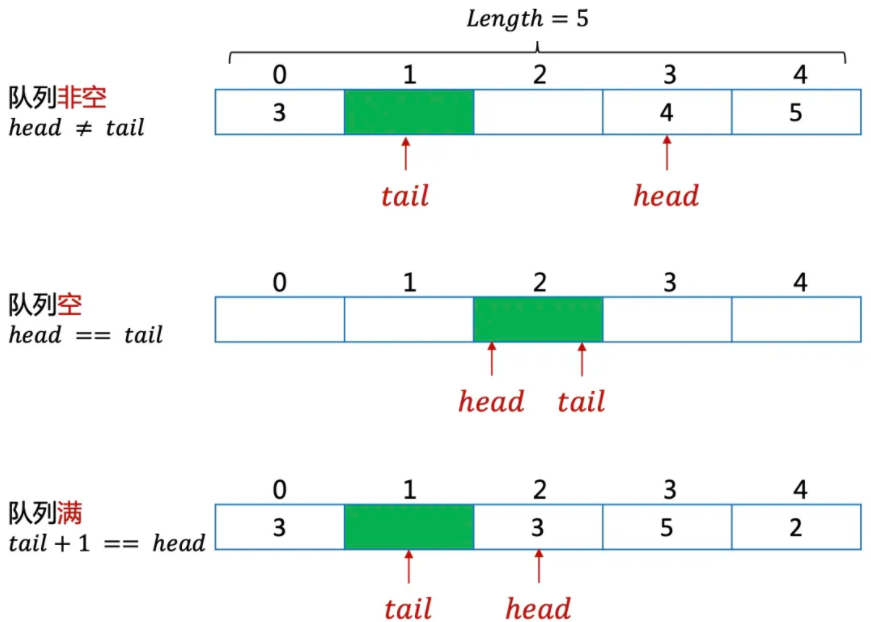
队列实现BFS

实现步骤如下：

• 将起点加入队列。

• 从队首取出一个节点，通过该节点向4个方向扩展子节点，并依次加入队尾。

• 重复以上步骤，直至队空或已找到目标位置。

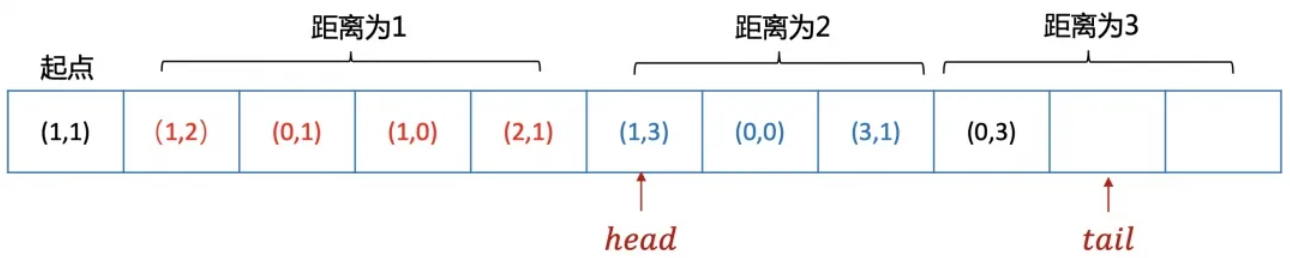
回归迷宫问题，到起点的距离为1,2,3...的点会依次入队。

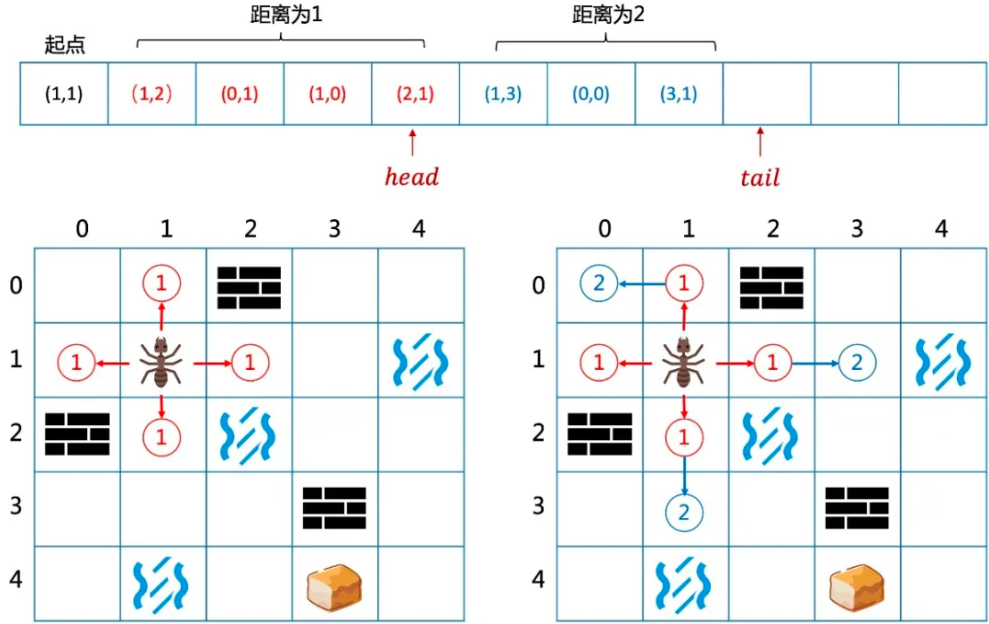
当head指针遍历到距离为2的点时，向4周扩展距离为3的节点，并继续入队。

未完待续